Bernoulli Spiral Clamps

[GarageWoodworks]

It's been a while since I've logged on here. Sorry!

Today I wanted to share with my NC woodworking buddies a new jig/clamp thingy that I made back in February.

You can see a video demo of the build and how they are used here. Hope you make a few and find them useful!

Would love to hear your thoughts on the clamp. If you've made a few already please let me know how you like them.

 

[Alan in Little Washington]

Ok, I admit to not being a mathematics historian or whatever, but isn't that a Fibonacci spiral (cam clamp), and not a Bernoulli spiral (cam clamp)?

Seems Woodpeckers made a similar mistake last month when they came out with what they called their Pythagoras square gauge.

 

[GarageWoodworks]

Ok, I admit to not being a mathematics historian or whatever, but isn't that a Fibonacci spiral (cam clamp), and not a Bernoulli spiral (cam clamp)?

Seems Woodpeckers made a similar mistake last month when they came out with what they called their Pythagoras square gauge.

No mistake. It is indeed a Bernoulli spiral. It is a Bernoulli spiral (logarithmic spiral) that happens to also grow outward by a factor of the golden ratio for every 90 degrees of rotation.

 

[GarageWoodworks]

Ok, I admit to not being a mathematics historian or whatever, but isn't that a Fibonacci spiral (cam clamp), and not a Bernoulli spiral (cam clamp)?

Seems Woodpeckers made a similar mistake last month when they came out with what they called their Pythagoras square gauge.

And Woodpeckers didn't make a mistake either. Their gauge is properly named because it utilizes the Pythagorean Theorem.

 

[Alan in Little Washington]

And Woodpeckers didn't make a mistake either. Their gauge is properly named because it utilizes the Pythagorean Theorem.

Well I guess we are both sorta right with respect to that spiral, it was a "favorite" of Bernoulli, though I suppose it might be more correct to call it a Descartes Spiral though it can also be traced back to 6th century India. Your drawing sure looks more like a Fibonnacci or Golden-ration-derived spiral (special case logarithmic spirals) than a pure logarithmic spiral. But without knowing how you made your template, I can't say.

As to the WP gauge, WP caught a bit of grief over the name. They even sent out a retraction of sorts, but didn't change the name even though it is NOT based on the pythagorean theorem (a[SUP]2[/SUP] + b[SUP]2[/SUP] = c[SUP]2)[/SUP]. It is geometry of circles (Theorem: an angle inscribed in a semi-circle is always a right angle).

Our friend the internet says:

----------------------------
This is the spiral for which the radius grows exponentially with the angle. The logarithmic relation between radius and angle leads to the name of logarithmic spiral or logistique (in French).

The distances where a radius from the origin meets the curve are in geometric progression.

The curve was the favorite of Jakob (I) Bernoulli (1654-1705). On his request his tombstone, in the Munster church in Basel, was decorated with a logarithmic spiral. The curve, which looks by the way more like an Archimedes' spiral, has the following Latin text accompanied: eadem mutata resurgo. In a free translation: 'although changed, still remaining the same'. This refers to the various operations for which the curve remains intact (see below). Therefore the curve is also called the Bernoulli spiral.

However, Rene Descartes (1638) was the first to describe and study the curve. Torricelli worked on the curve independently, and found the curve's length. The curve is also named to Fibonacci as the Fibonacci spiral.

--------------------------------

 

[GarageWoodworks]

Well I guess we are both sorta right with respect to that spiral, ...
--------------------------------

Yes - the spiral is both a Bernoulli spiral and a golden spiral. All golden spirals are Bernoulli spirals but not all Bernoulli spirals are golden spirals.

Stolen from the net: "In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes."

Back to Woodpeckers:
I don't understand how their gauge violates being called a Pythagoras Gauge. a2 +b2 = c2 for a right triangle always holds true. The longer side of their tool is c2 and the distances between the contact points formed by the pivot make up a2 and b2. Their tool is aptly named.

 

[Jeremy Scuteri]

Yes - the spiral is both a Bernoulli spiral and a golden spiral. All golden spirals are Bernoulli spirals but not all Bernoulli spirals are golden spirals.

Stolen from the net: "In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes."

Back to Woodpeckers:
I don't understand how their gauge violates being called a Pythagoras Gauge. a2 +b2 = c2 for a right triangle always holds true. The longer side of their tool is c2 and the distances between the contact points formed by the pivot make up a2 and b2. Their tool is aptly named.

Of course you can take the right angle being measured with the woodpeckers tool and label a2, b2 and c2. That is always possible since it is a right triangle. That is however different from saying that this tool is "USING the pythagorean theorem". It is not measuring a or b. It is however tracing out an arc with the center leg. Semantics to a certain extent...

 

[GarageWoodworks]

Of course you can take the right angle being measured with the woodpeckers tool and label a2, b2 and c2. That is always possible since it is a right triangle. That is however different from saying that this tool is "USING the pythagorean theorem". It is not measuring a or b. It is however tracing out an arc with the center leg. Semantics to a certain extent...

It uses the theorem because in order for you to have a right triangle, the distance a2 + b2 must equal c2. That is Pythagoras. There is no arc being traced that is required for the process.

 

[junquecol]

Thanks for the education. All these years, I been calling those things cam clamps, but no more. I EDUCATED now!

 

[GarageWoodworks]

Thanks for the education. All these years, I been calling those things cam clamps, but no more. I EDUCATED now!

Smart guy eh? So you've been using these in your woodworking all these years?

 

[TedAS]

Well this was fun to read!
I made thoes cam clamps about 25 years ago. Used them hard, lost them, and forgot about them. Thanks for reminding me to make more.

 

[Jeremy Scuteri]

It uses the theorem because in order for you to have a right triangle, the distance a2 + b2 must equal c2. That is Pythagoras. There is no arc being traced that is required for the process.

"in order for you to have a right triangle, the distance a2 + b2 must equal c2"
Absolutely true. Nobody is arguing that point. While that property will always hold true, it doesn't mean that it is utilized by the tool. There are other ways to verify or create right angles that don't UTILIZE that property. Consider the case when the diagonals are measured in a box. This verifies 4 right angles, but doesn't use a2+b2=c2. Consider the perpendicular bisector with a compass and straight edge, this creates 2 right angles without pythagoras. An arc being traced is not REQUIRED, but it is the property that the woodpecker tool EXPLOITS to verify a right angle in this case. The center leg of the tool (what you labeled b2) traces an arc/semicircle as you rotate it. This is the semicircle that a previous poster was eluding to. Again, I stress the point that the tool does not actually measure a or b and therefore does not USE pythagoras for this. Will a2+b2=c2 still hold true for the right angle? Of course it will. Just like measuring the diagonals of a box will allow you to verify 4 right angles without measuring a single angle. All the angles must be 90 degrees, but you don't have to use a tool that measures 90 degree angles to verify this.

 

[GarageWoodworks]

"Absolutely true. Nobody is arguing that point. While that property will always hold true, it doesn't mean that it is utilized by the tool."

Ridiculous.

 

[Alan in Little Washington]

"Absolutely true. Nobody is arguing that point. While that property will always hold true, it doesn't mean that it is utilized by the tool."

Ridiculous.

Well dang, I just lost a very long thread when my mouse fell into my lap :BangHead: :BangHead: :BangHead: :BangHead:

Here is the short version of the WP gauge part-

If you don't believe other posters, believe Woodpeckers themselves. After catching a lot of grief over the name, Woodpeckers sent out a follow-up email about the "Pythagoras Gauge" wherein they admitted that the principle behind its operation is actually the Thales Theorem. Since it was a "One Time Tool" they didn't change the name.

In the diagram above, the long arm of the WP gauge equates to AC. The short arm to the distance OB. The distance from the pivot point to all tips is equal just like in the circle (OA = OB = OC) so AC is a diameter and OB is a radious. So if tips of the long arm ( A & C) touch the sides of an opening and the tip of the movable arm (B) is seated in the corner, then the inscribed angle created by the sides of the opening (AB and BC) by geometric proof is a right angle (90 degr.). There is no squaring of sides or measurements. Pythagoras did a lot of good things, but didn't play in this game.

 

[GarageWoodworks]

You're splitting hairs. Thales isn't needed here. If there were no Thales theorem we could still design the tool because of Pythagoras's work.

All we need to know is c2 = a2 +b2 and Badda Bing! We have the tool. W/o Pathag and Thales you'd be in trouble.

If the tool designer at Woodpeckers never heard of Thales and only new of Pathag he would get to the tool through Pathag (as likely the process was).

To say that Pathag isn't utilized in this tool is absurd.

 

[Alan in Little Washington]

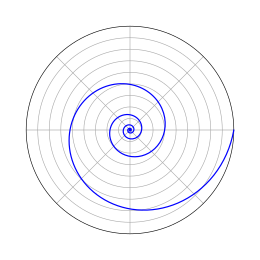
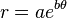Yes - the spiral is both a Bernoulli spiral and a golden spiral. All golden spirals are Bernoulli spirals but not all Bernoulli spirals are golden spirals.

Stolen from the net: "In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes."

Well sorta. Bernoulli was a big fan of logarithmic spirals, but not all spirals are logarithmic. It depends on how it is generated. To be both a logarithmic and golden ratio it must use the golden ratio in the logarithmic equation. The golden ratio is not a finite number, but approximated. In fact most spirals that claim to be logarithmic are just approximations. Most are good enough for government work, but not true logarithmic spirals which must be drawn with the help of a computer. As you already know the shape of a logarithmic spiral depends on a variable that in the case of a golden spiral is the golden ratio. It is usually drawn in polar coordinates using the following equation:

(b is the "growth factor" and equals the golden ratio)

So, depending on how you made your template, you may not have actually used a Bernoulli (logarithmic) Spiral. Judging by your template which includes rectangles, it is quite possible you used one of the approximations. There are several similar spirals that approximate, but do not exactly equal, a golden spiral. These are often confused with the golden spiral. For example, a golden spiral can be approximated by a "whirling rectangle diagram," in which the opposite corners of squares formed by spiraling golden rectangles are connected by quarter-circles. The result is very similar to a true golden spiral.

Approximate and true golden spirals: the green spiral is made from quarter-circles tangent to the interior of each square, while the red spiral is a golden spiral, a special type of logarithmic spiral. Overlapping portions appear yellow. The length of the side of a larger square to the next smaller square is in the golden ration:

Another approximation is a Fibonacci spiral, which is not a true logarithmic spiral. It is made up of a series of quarter-circular arcs whose radii are consecutively increasing Fibonacci numbers. Every quarter turn a Fibonacci spiral gets wider not by φ, but by a changing factor that equals the ratio of a term in the Fibonacci sequence to its predecessor. The ratios of consecutive terms in the Fibonacci series approach φ, so that the two spirals are very similar in appearance.

A Fibonacci spiral approximates the golden spiral; unlike the "whirling rectangle diagram" based on the golden ratio, above, this one uses quarter-circle arcs inscribed in squares of integer Fibonacci-number side, shown for square sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34.

Both approximations sure look a lot like your template. If your template used the logarithmic formula it wouldn't need the rectangles used by the approximations. The approximations are sure a lot easier to generate!!

Aren't you glad you decided to visit? Cam clamps, whether Fibonacci, Bernoulli, Descartes-based, etc. can be very useful in a lot of applications. Yours look useful, and appear simple and inexpensive to make. Thanks for posting!

 

[Alan in Little Washington]

You're splitting hairs.

To say that Pathag isn't utilized in this tool is absurd.

Nope, and nope. Just plane geometry without Pythagoras (pun intended.)

Show were the Pythagorean Theorem comes into play with the WP gauge, not with a right angle but with the gauge- remember there are no dimensions on this gauge, it can be any size, and the long bar can be placed at any slope inside the opening. Time to break out the old HS Geometry book.

 

[GarageWoodworks]

Well sorta. Bernoulli was a big fan of logarithmic spirals, but not all spirals are logarithmic.

I never claimed all spirals were logarithmic.

Both approximations sure look a lot like your template. If your template used the logarithmic formula it wouldn't need the rectangles used by the approximations. The approximations are sure a lot easier to generate!!

Not unless the rectangles were used to generate the Fibbonnacci numbers from my Bernoulli spiral which grew at a rate of one golden ratio per 1/4 turn.

Aren't you glad you decided to visit? Cam clamps, whether Fibonacci, Bernoulli, Descartes-based, etc. can be very useful in a lot of applications. Yours look useful, and appear simple and inexpensive to make. Thanks for posting!

Aside from utilizing a cam as a clamp is there a reason why you posted the pics below?

 

[Alan in Little Washington]

I never claimed all spirals were logarithmic.

No, but according to all sources, Bernoulli spirals (Spira mirabilis) were all logarithmic.

Not unless the rectangles were used to approximate the Fibbonnacci numbers on my Bernoulli spiral which grew at a rate one golden ratio per 1/4 turn.

You are missing the point, if you used rectangles or Fibonacci numbers, then you didn't draw a logarithmic spiral and therefore didn't draw a Bernoulli spiral. QED

Aside from utilizing a cam as a clamp is there a reason why you posted the pics below?

Nope.

 

[GarageWoodworks]

No, but according to all sources, Bernoulli spirals (Spira mirabilis) were all logarithmic.

And?

You are missing the point, if you used rectangles or Fibonacci numbers, then you didn't draw a logarithmic spiral and therefore didn't draw a Bernoulli spiral. QED

Nope.

You are missing the point friend.

One can draw a golden spiral, a logarithmic spiral that grows outward by a factor of the golden ratio for every 90 degrees of rotation (pitch about 17.03239 degrees).
You could then draw rectangles on the spiral to demonstrate that the Fibonacci numbers are very closely obeyed.